Upsampling |
|||||
Päivitetty 6.8.2000 Mitä on upsampling?(käytetään myös termejä up-conversion ja eräissä yhteyksissä oversampling) Upsamplingillä tarkoitetaan alkuperäisen pulssikoodimoduloidun signaalin ylinäytteistämistä korkeammalle näytteenottotaajuudelle ja sananpituuden interpoloimista suuremmalle bittiluvulle. Upsampling tapahtuu pääpiirteissään neljässä vaiheessa (1)
Upsamplingin periaate
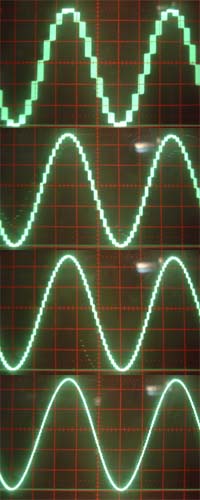
Kuva: MSB Technology Upsamplingin yhteydessä ylinäytteistystaajuuksille syntyneet alkuperäisen signaalin kuvajaiset voidaan suodattaa loivalla alipäästösuotimella, tällöin suodatuksen kuuloalueelle ulottuva haitallinen vaikutus vähenee. Upsamplingin vaikutukset äänenlaatuunKun analogisignaalin alipäästösuodatus tapahtuu hyvän matkaa kuuloalueen yläpuolella, voidaan käyttää loivempaa alipäästösuodatusta, haitalliset vaikutukset vähenevät kuultavalla alueella, joka ilmenee ylärekisterin sävykkyytenä ja luonnollisuutena. Toisaalta matalatasoisten signaalien tarkkuus paranee upsamplingin vaikuttaessa kvantisointivirheen vähentymiseen.
Upsampling ei kuitenkaan palauta sellaista alkuperäistä informaatiota, joka on peruuttamattomasti kadonnut äänitteen tuotannon eri vaiheissa. Balanced Audio Technologyn kuuluisa suunnittelija Victor Khomenko vertasi upsamplingia freskojen entisöintiin: Rappeutuneen maalauksen puutuvat palat täydennetään sen informaation perusteella mitä säilyneessä osassa on käytettävissä. Entisöinti ei palauta alkuperäistä, puutuvaa informaatiota, mutta maalaus on saanut uskottavan olemuksen, joka on rappeutunutta alkuperäistä ylevämpi. Juuri tästä on kysymys upsamplingissä: puutteellista signaalia täydennetään uskottavalla informaatiolla sen perusteella mitä ympäröivästä informaatiosta voidaan päätellä ja lopputulos on vakuuttavampi kuin alkuperäisellä, mutta puutteellisella signaalilla. Max Hauserin selostus upsamplingistäBob Ohlsson on ystävällisesti postittanut oheisen artikkelin, joka on ilmestynyt alunperin usenetissä 1991 rec.audio.high-end uutisryhmään: IntroductionThis is a broad and
not-very-technical online summary of CD If you want more depth of information on these topics, my colleague Prasanna Shah recently published a dense technical overview of audio oversampling in the popular magazine Audio in January. I published a long technical tutorial (not specific to CD or DAT products) in the Journal of the Audio Engineering Society, January/February 1991 (vol. 39 no. 1/2 pp. 3-26). A lighter and shorter overview of mine is also available as Preprint #2973 from the Audio Engineering Society, 60 East 42nd Street, New York, New York 10165 USA, Telephone 212-661-8528, FAX 212-682-0477. This preprint was recently recommended by the popular magazine Stereophile. AES charges $5 for such preprints ($4 for members), $3 for journal-article copies and $10 for back issues, and is pretty efficient about getting them into your hands if you FAX them a request with V. or MC. credit-card information (I did so recently and the copies arrived in the mail in about three days). These papers contain many further references. Some of these sources emphasize the A/D rather than D/A path but the core principles are identical (the circuit implementation of each section interchanges between analog and digital). Do not be alarmed if the following summary takes an approach different from what you read elsewhere. There are details here not usually mentioned in popular summaries (or even in the research literature). A. Thumbnail Sketch of Oversampling (Upsampling)Signals such as audio, stored digitally, entail a finite *sampling rate* (44.1 kilosamples/sec for the 12-cm CD) whereas in their natural (analog) form they are continuous-time waveforms (you can think of this usefully as an "infinite" sampling rate). The circuitry that regenerates the continuous-time analog output in a CD player has two major tasks: translating a stream of digital numbers into analog values ("conversion") and also bridging between the finite sampling rate of the digital sequence and the "infinite" sampling rate of the outside world (that is, restoring a correct continuous waveform from discrete samples) -- "reconstruction." Non-oversampling conversion-reconstruction (C-R) systems make the transition from finite to "infinite" sampling rate in one step, while oversampling systems do it through one or more intermediate sampling rates (higher than the original, but still finite). Although the details may not be obvious at this point, producing these intermediate signals with elevated sampling rates is a purely digital process and can thus be performed predictably and repeatably (although it does require that you have technologies where digital logic is very cheap, and therefore it was unattractive until recent years, although the basic techniques have been known since the 1950s and in embryonic forms since the time of the second world war). Not only the reconstruction process but also separately the conversion process (bits into volts) benefits from the use of an intermediate sampling rate on the way to continuous time. Designers can orchestrate eloquent mathematical tricks to trade a higher deliberate sampling rate for lower required resolution in internal digital-to-analog converter (DAC) circuitry. This in turn tends to render the analog part of the C-R chain simpler and more tolerant of component fluctuations. But moreover, in practice oversampling C-R systems blend the two tasks of conversion and reconstruction so that they overlap in actual hardware, unlike a classical, non-oversampling system. The subjects of this paragraph are extremely complex and seductively counterintuitive even to well-trained engineers, and they habitually garner the most imaginative misinterpretations in popular-press writing. An oversampling conversion-reconstruction (C-R) system in practice normally contains a series of four major blocks. The first is a sampling-rate- increasing digital filter, the second a digital quantization-management subsystem or "noise-shaping modulator," the third a DAC circuit _per se_ and the fourth an analog lowpass filter. A classical, or non-oversampling, system lacks the first two blocks, but is far more demanding of the last two blocks, which are analog circuits that largely determine the performance and subtler behaviors of the signal path. (That's the whole reason for oversampling, in a nutshell.) By the way, these four blocks
reflect a combination of traditionally separate specialties in electrical engineering,
each with a different intuition and set of assumptions about what is technically difficult
or important. This is why you will find many different explanations of oversampling
(some of them seemingly in conflict) even from competent specialists. The first of
the four blocks is generically a digital filter, the second a quantizer (or quantized
feedback system), the third a precision analog circuit and the fourth an analog filter,
and most or all are realized in integrated circuitry. Thus, for example, someone
familiar with digital filtering will usually focus on the first of the four blocks, and
when asked for more information will B. InterpolatorThe first block, the sampling-rate-increasing digital filter, in an oversampling C-R system is commonly nicknamed an "interpolator." This jargon is triply unfortunate. First, almost everybody unfamiliar with multirate digital filtering assumes from the name, incorrectly, that this block performs "interpolation" in the common mathematical sense (such as linear or polynomial interpolation between data points). Actually the name is a specialized digital-filtering coinage subtly but crucially different. Second and third, as if that weren't trouble enough, the term "interpolative" is sometimes applied in two further ways to oversampling C-R systems (one of these usages is a subset of the other). More details about this and other glorious terminological pitfalls are in my recent AES Journal paper. Here is the briefest sketch of how the rate-increasing filter works. The objective is to convert a signal at a sampling rate like 44.1 ks/s to a signal at a higher sampling rate *without* changing the information content. Mathematically this is a well-defined and tractable problem. If you just take the original sequence of samples and insert after each of them, for example, three new samples (with value zero, or holding the last old-sample value, or almost anything else intelligent) then you will obtain a new sequence at four times the original rate. In frequency spectrum this new sequence will however include new high-frequency replicas (images) of the original signal's spectrum. A digital lowpass filter will remove these images and leave a signal spectrally identical to the original. In the time domain, you will now see a higher-rate sequence that will look like the original but with the "right" new samples smoothly inserted between old. (In actual practice the "insertion" of new samples is NOT a separate step as above, but is incorporated into the digital-filter arithmetic.) C. Multibit vs. single-bit vs. MASH etc.All four of the major blocks of
an oversampling C-R system, outlined in Section A, admit endless variations, opportunities
for design
Each of these competing modulator topologies has technical strengths and weaknesses that are very involved and do not lend themselves to summary. The signal fidelity in each of them can be excellent but depends on different sets of circuit elements. It is all a matter of "second-order" electrical effects; if the components are all perfect (as they invariably are assumed to be, in popular explanations of this subject matter), then all the techniques work equally well. Very broadly, however, I would say that the one-bit designs have the fewest subtle distortion vulnerabilities. D. What does it mean for soundThe electrical specifications of
an oversampling C-R system depend on innumerable component values and design choices and
are in no way simply predictable from whether the internal modulator uses, for example,
MASH or Bitstream or some other topology. Still less Notes from the textNote 1: "Delta-sigma" modulation and data conversion (the inventors' term) was unintentionally rechristened "sigma-delta" at the Bell Telephone Laboratories in 1963 and this reversal has propagated through many paper titles, so you will see both names in use. No difference is intended. I have made efforts to redress this reversal and the principals are now in accord. My recent JAES paper mentions this and I have further details if anyone professionally interested sends a mailing address. Note 2: Some people dislike the acronym MASH for MultistAge noise SHaping, though there certainly are endless well-known precedents (UNIted nations ChildrEn's Fund; GEheime STAatsPOlizei). When its coiners introduced "MASH" in the US in 1986 a colleague remarked to me that MUSH was better on acronym style. I think however that MUSH would have less audio-marketing cachet. The technique now dubbed "MASH" by NTT has existed in various forms since long before its recent popularization by Toshio Hiyashi et al. in February 1986 (this origin itself is usually misattributed to a later paper by Uchimura et al.). I have antecedents going back at least to 1969. Multibit feedback noise shaping is even older, due to Cutler in 1954. Max W. Hauser {mips,philabs,pyramid}!prls!max prls!max@mips.com Copyright (c) 1991 by Max W. Hauser. All rights reserved.
|